Finite-state mesin dapat model sejumlah besar masalah, di antaranya adalah desain otomatisasi elektronik , protokol komunikasi desain, parsing dan aplikasi rekayasa lainnya. Dalam biologi dan kecerdasan buatan penelitian, negara bagian mesin atau hirarki dari mesin negara kadang-kadang digunakan untuk menggambarkan sistem saraf , dan dalam linguistik mereka dapat digunakan untuk menggambarkan tata bahasa alami bahasa .
Model Matematika
- Sebuah mesin negara deterministik finite atau akseptor deterministik mesin negara yang terbatas adalah berlipat lima
 , Dimana:
, Dimana:  adalah input alfabet (a, hingga non-kosong set simbol).
adalah input alfabet (a, hingga non-kosong set simbol). 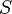 adalah, hingga non-kosong set negara.
adalah, hingga non-kosong set negara.  adalah keadaan awal, unsur
adalah keadaan awal, unsur 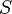 .
.  adalah fungsi negara transisi:
adalah fungsi negara transisi:  (Dalam otomat terbatas nondeterministic akan
(Dalam otomat terbatas nondeterministic akan  , Yaitu,
, Yaitu,  akan kembali satu set negara).
akan kembali satu set negara). 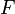 adalah himpunan negara akhir, subset (mungkin kosong) dari
adalah himpunan negara akhir, subset (mungkin kosong) dari 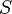 .
.
 menjadi fungsi parsial , yaitu
menjadi fungsi parsial , yaitu  tidak harus didefinisikan untuk setiap kombinasi
tidak harus didefinisikan untuk setiap kombinasi  dan
dan  . Jika FSM
. Jika FSM 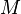 ini dalam keadaan
ini dalam keadaan  , Simbol selanjutnya adalah
, Simbol selanjutnya adalah  dan
dan  tidak didefinisikan, maka
tidak didefinisikan, maka 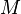 bisa mengumumkan kesalahan (yaitu menolak input). Hal ini berguna dalam definisi mesin negara umum, tetapi kurang berguna ketika mengubah mesin. Beberapa algoritma dalam bentuk standar mereka mungkin memerlukan fungsi total.
bisa mengumumkan kesalahan (yaitu menolak input). Hal ini berguna dalam definisi mesin negara umum, tetapi kurang berguna ketika mengubah mesin. Beberapa algoritma dalam bentuk standar mereka mungkin memerlukan fungsi total. Sebuah mesin finite-state adalah terbatas mesin Turing mana kepala hanya dapat melakukan "membaca" operasi, dan selalu bergerak dari kiri ke kanan.
- Sebuah transduser negara yang terbatas adalah sextuple
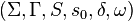 , Dimana:
, Dimana:  adalah input alfabet (satu set kosong hingga non simbol).
adalah input alfabet (satu set kosong hingga non simbol).  adalah abjad keluaran (a, hingga non-kosong set simbol).
adalah abjad keluaran (a, hingga non-kosong set simbol). 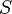 adalah, hingga non-kosong set negara.
adalah, hingga non-kosong set negara.  adalah keadaan awal, unsur
adalah keadaan awal, unsur 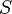 . Dalam sebuah robot yang terbatas nondeterministic ,
. Dalam sebuah robot yang terbatas nondeterministic ,  adalah seperangkat negara awal.
adalah seperangkat negara awal.  adalah fungsi negara transisi:
adalah fungsi negara transisi:  .
.  adalah fungsi output.
adalah fungsi output.
 ) Definisi yang sesuai dengan model Mealy, dan dapat dimodelkan sebagai mesin Mealy . Jika fungsi keluaran hanya bergantung pada negara (
) Definisi yang sesuai dengan model Mealy, dan dapat dimodelkan sebagai mesin Mealy . Jika fungsi keluaran hanya bergantung pada negara (  ) Definisi yang sesuai dengan model Moore, dan dapat dimodelkan sebagai sebuah mesin Moore . Sebuah mesin finite-state tanpa fungsi output sama sekali dikenal sebagai semiautomaton atau sistem transisi .
) Definisi yang sesuai dengan model Moore, dan dapat dimodelkan sebagai sebuah mesin Moore . Sebuah mesin finite-state tanpa fungsi output sama sekali dikenal sebagai semiautomaton atau sistem transisi . Jika kita mengabaikan simbol keluaran pertama dari mesin Moore,
 , Maka dapat dengan mudah dikonversi ke mesin Mealy output-setara dengan menetapkan fungsi output dari setiap transisi Mealy (yaitu pelabelan setiap tepi) dengan simbol output tertentu dari negara tujuan Moore. Transformasi Kebalikannya kurang jelas karena keadaan mesin Mealy mungkin memiliki label output yang berbeda pada transisi masuk nya (pinggiran). Setiap negara bagian tersebut perlu untuk dibagi di beberapa mesin Moore menyatakan, satu untuk setiap simbol keluaran insiden.
, Maka dapat dengan mudah dikonversi ke mesin Mealy output-setara dengan menetapkan fungsi output dari setiap transisi Mealy (yaitu pelabelan setiap tepi) dengan simbol output tertentu dari negara tujuan Moore. Transformasi Kebalikannya kurang jelas karena keadaan mesin Mealy mungkin memiliki label output yang berbeda pada transisi masuk nya (pinggiran). Setiap negara bagian tersebut perlu untuk dibagi di beberapa mesin Moore menyatakan, satu untuk setiap simbol keluaran insiden. 












Tidak ada komentar:
Posting Komentar